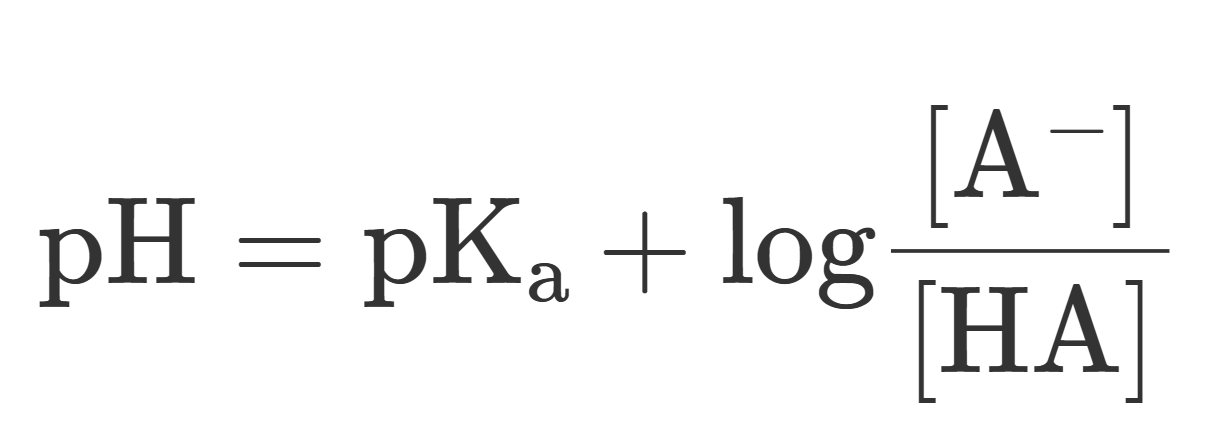ヘンダーソン・ハッセルバルヒの式

　この記事では， K_a（酸解離定数）を用いたpHの求め方を紹介したいと思います．つまり，ヘンダーソン・ハッセルバルヒの式の利用と導出方法の紹介です．

酸解離定数

　はじめに，酢酸（CH₃COOH）などのように分子１個につき，１個の水素イオン（H⁺）を放出する酸を一塩基酸といいます．このような一塩基酸の化学式を一般式化してHAと置きます．すると，そのHAの解離は以下の化学反応式で表すことができますね．

$$\rm{HA}+\rm{H_2O} \rightleftharpoons \rm{A^-} + \rm{H_3O^+}$$

そして，HAの解離定数（K_a）は次のように定義されます．

$$ \rm{K_a} = \frac{[H^+] [A^-]}{[HA]} $$

念のため補足しておくと，[ ] はそれぞれの濃度を示します．例えば [ HA ] は「HAの濃度」という意味になります．

確認クイズ１

　ギ酸の解離定数（K_a）を表す式を書いてください．

確認クイズ１の解答例

　先ほどの例にならって以下のように表すことができます．

$$ \rm{K_a} = \frac{[H^+] [HCOO^-]}{[HCOOH]} $$

酸解離定数の説明は以上になります．

酸解離指数

　続いては，酸解離指数の説明ですが，本題に入る前に高校化学の内容を軽く確認しておきましょう．高校化学では，水素イオン濃度 [H⁺] を用いてpHを求める方法として以下の公式を学習しました．

$$ \rm{pH} = -log_{10} [H^+] $$

これを踏まえた上で本題に入りたいと思います．さて，本題の酸解離指数（pK_a）ですが，何となく上のpHと似ているとは思いませんか？　実は，pK_aもpHと同様にK_a（酸解離定数）を用いて以下の公式で表すことができます．

$$ \rm{pK_a} = -log_{10} K_a $$

　大学化学ではlog₁₀の場合，底を省略して単にlogと書くことが多いので，それにならって以下log₁₀の場合は底を省略します．

本当に公式までpHとそっくりですね！

確認クイズ２

酢酸の酸解離指数（pK_a）を求めてください．ただし，酢酸の酸解離定数（K_a）の値は\(1.8 \times 10^{-5}\) とします．また，\(\rm{log} 1.8 \simeq 0.26\) とします．

確認クイズ２の解答例

先ほどの公式に代入するだけで簡単に求められますね．

$$ \rm{pK_a} = 5-log 1.8 =4.74 $$

酸解離定数の説明は以上になります．

ヘンダーソン・ハッセルバルヒの式を導出する

　大変お待たせ致しました！ ここで，本記事の本題であるヘンダーソン・ハッセルバルヒの式を導出（導出というほどでもありませんが…）したいと思います．先に結論（公式）を書きます．

$$ \rm{pH} = pK_a + log \frac{[A^-]}{[HA]} $$

このように短い式ですので，覚えるのも苦ではありませんが，前述の酸解離定数，酸解離指数の式を使うと簡単に導出することができます．以下に導出の手順を示します．

Kaの式を変形する

$$ \rm{K_a} = \frac{[H^+] [A^-]}{[HA]} $$

の式を次のように変形します．

$$ \rm{[H^＋] = \frac{K_a [HA]}{[A^-]}} $$

両辺の対数をとって変形する

　上の式で両辺の対数をとって変形すると，以下のようになります．

$$ \rm{pH} = pK_a + log \frac{[A^-]}{[HA]} $$

以上で導出完了になります．

まとめ・補足と確認問題

今回の記事で登場した数式をまとめます．

$$ \rm{K_a} = \frac{[H^+] [A^-]}{[HA]} $$

$$ \rm{pK_a} = -log_{10} K_a $$

$$ \rm{pH} = pK_a + log \frac{[A^-]}{[HA]} $$

補足

　さて，上記でヘンダーソン・ハッセルバルヒの式を示しましたが，さらにここから近似を用いて式を変形すると緩衝液のpHを求める式を導出することができます．

弱酸HAと強塩基からなる濃度c_sの塩と濃度c_aの弱酸で構成される緩衝液のpHを求める式は，ヘンダーソン・ハッセルバルヒの式を用いて次のように近似できます．

$$ \rm{pH} \simeq pK_a + log \frac{c_s}{c_a} $$

確認問題

　濃度比が1:3の酢酸と酢酸ナトリウムの混合水溶液のpHを求めてください．ただし，酢酸の酸解離指数は，4.74とします．また，必要に応じて log 2 = 0.30，log 3 = 0.48 として計算してください．

確認問題の解答例

　問題文の条件より，[c_a]:[c_s]=1:3 であることが分かります．これをヘンダーソン・ハッセルバルヒの式の変形バージョンに代入すると，以下のようになりますね．

$$ \rm{pH} = pK_a+log \frac{[c_s]}{[c_a]} = 4.74 + log \frac{3}{1} $$

よって，log 3 = 0.48 を用いて計算すると，pH = 4.74 +0.48 = 5.22 と求めることができます．